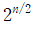SE 05) 1. 일방향 해시함수의 개요

리네양 2023. 6. 16. 23:12

(1) 일방향 해시함수의 개요

1) 기본 개념

① 해시함수는 임의의 길이를 갖는 메시지를 입력으로 하여 고정된 길이의 해시값 또는 해시 코드라 불리는 값을 출력하는 함수이다. 보다 엄밀하게 말하면, 해시함수 h는 임의의 길이의 문자열을 고정된 길이를 갖는 n비트 문자열로 대응시킨다.

② 정의역을 D, 치역을 R이라고 할 때 해시함수 h : D→R( |D| > |R| )는 다대일 대응 함수이다. 이것은 충돌이 반드시 존재함을 의미한다.

2) 일방향 해시 함수의 특징

① 임의의 길이의 메시지로부터 고정 길이의 해시값을 계산한다.

⊙ 어떤 길이의 메시지를 입력으로 주더라도 항상 짧은 해시값을 생성하지 않으면 의미가 없다.

② 해시값을 고속으로 계산할 수 있다.

⊙ 해시값을 구하기 위해 시간이 너무 오래 걸리면 안 된다.

③ 일방향성을 갖는다.

⊙ 일방향 해시함수는 일방향성(one-way)을 가질 필요가 있다. 이것은 해시값으로부터 메시지를 역산할 수 없다는 성질이다.

[ M : 메시지 ] → >[해시 함수]< → [ H(M) ]

[ M : 메시지 ] ←------------- x ------------- [ H(M) ]

해시 값으로 부터

메시지를 구할 수는 없다.

④ 메시지가 다르면 해시값도 다르다.

⊙ 무결성을 확인하기 위해 사용한다. 메시지가 1비트라도 변화하면 해시값은 매우 높은 확률로 다른 값이 되어야 하기 때문이다.

⊙ 2개의 다른 메시지가 같은 해시값을 갖는 것을 충돌(collision)이라고 한다. 일방향 해시 함수를 무결성 확인에 사용하기 위해서는 충돌이 발견되어서는 안 된다.

[ 메시지A ] → >[해시 함수]< → [ H(A) ]

[ 메시지B ] → >[해시 함수]< → [ H(B) ]

A ≠ B 동일한 해시 함수 다른 해시 값(H(A) ≠ H(B))

⊙ 충돌을 발견하는 것이 어려운 성질을 가리켜 충돌 내성(collision resistance)*이라고 부른다. 암호 기술에서 사용되는 일방향 해시함수는 충돌 내성을 가질 필요가 있다.

* 충돌 방지(내성)

- 해시 함수에서 충돌 방지 특성이란 이러한 충돌을 찾기 어렵도록 하는 것이다.

(2) 해시 함수의 분류와 보안 요구사항

1) 해시 함수의 보안 요구사항

(A) 개요

① 암호학적 해시 함수는 프리이미지 저항성(preimage resistance), 제2프리이미지 저항성(second preimage resistance), 충돌 저항성(collision resistance)의 3가지 기준을 충족해야 한다.

(B) 프리이미지 저항성(역상 저항성)

① 해시값 h = H(x)에 대하여, x는 h의 선 이미지(preimage)라 한다. 즉, x는 함수 H를 사용한 해시 함수 결과가 h인 데이터 블록이다. H가 다대일 대응이므로, 주어진 해시값 h에 대하여 여러 개의 선 이미지가 존재하게 된다.

② 암호학적 해시 함수는 프리이미지 저항성이 있어야만 한다.

③ 프리 이미지* 저항성이란 주어진 해시 함수 h와 y = h(M)에 대해서 이브가 y = h(M')를 만족하는 메시지 M을 찾아낸다는 것이 매우 힘들어야 한다는 성질이다. (프리 이미지 저항성은 일방향성임)

* 프리 이미지

f(x) = y에서 x는 y의 이전 이미지라고 한다. f가 일대일 대응이 아니면, 하나의 y에 여러 개의 이전 이미지가 있을 수 있다.

① 두 번째 기준은 제2프리이미지 저항성으로, 메시지를 쉽게 위조할 수 없도록 하는 성질이다.

② 이브는 메시지 M과 다이제스트 h(M)을 가로챈다. 이브는 h(M) = h(M')를 만족하는 다른 메시지(M')를 생성한다. 이브는 M'와 h(M')을 밥에게 보낸다. 이브는 이렇게 해서 메시지를 위조할 수 있는 것이다.

③ 이런 충돌이 발생할 확률은 충돌 저항성(강한 충돌 내성)보다 상대적으로 낮기 때문에 약한 충돌 내성이라 한다.

(D) 충돌 저항성(충돌 회피성, 강한 충돌 내성)

① 세 번째는 충돌 저항성(collision resistance)이다. 이것은 이브로 하여금 동일한 다이제스트를 가지는 2개의 메시지를 구하지 못하도록 하는 것이다. 여기서 공격자는 어떤 정보도 없는 상태에서 동일한 다이제스트를 갖는 두 개의 메시지를 생성할 수 있다.

② 충돌이 발생할 확률은 약한 충돌 내성의 경우보다 상대적으로 높기 때문에 강한 충돌 내성이라 한다.

중요 체크!

▶ 해시 함수가 가져야 할 성질

⊙ 역상 저항성 : 주어진 임의의 출력값 y에 대해 y = h(x)를 만족하는 입력값 x를 찾는 것이 계산적으로 불가능하다.

⊙ 두 번째 역상 저항성 : 주어진 입력값 x에 대해 h(x) = h(x'), x≠x'을 만족하는 다른 입력값 x'을 찾는 것이 계산적으로 불가능하다.

⊙ 충돌 저항성 : h(x) = h(x')을 만족하는 임의의 두 입력값 x, x'을 찾는 것이 계산적으로 불가능하다.

요구사항	설명
다양한 입력 길이	H는 어떤 크기의 데이터 블록에도 적용될 수 있다.
고정된 출력 길이	H는 고정된 크기의 출력을 만든다.
효율성	H(x)는 실질적으로 하드웨어 및 소프트웨어에 적용하기 용이하여야 하며, 어떠한 x에 대해서도 계산이 비교적 수월해야 한다.
선이미지 회피성(일 방향성)	어떠한 코드 h에 대해서도 H(x) = h인 x를 찾는 것은 계산적으로 실행 불가능하다.
2차 선이미지 회피성 (약한 충돌 회피성)	어떠한 블록 x에 대해서도, H(y) = H(x)인 y(≠ x)인 것을 찾는 것이 계산적으로 실행 불가능하다.
충돌 회피성 (강한 충돌 회피성)	H(x) = H(y)인 어떤 (x, y) 짝을 찾는 것이 계산적으로 실행 불가능하다.

암호학적 해시함수의 요구사항

2) 전자서명에 이용되는 해시 함수의 특성

① 해시값을 고속으로 계산할 수 있다.

⊙ 해시값을 구하기 위해 걸리는 시간이 너무 길어지면 안 된다.

⊙ 메시지가 길어져서 해시값을 구하는 시간이 길어지는 것은 어쩔 수 없지만 현실적인 시간 내에 계산할 수 없다면 소용이 없다.

② 약 일방향성 (Weak onewayness)

⊙ 해시값 H로부터 h(M) = H가 되는 서명문 M을 찾는 것은 계산상 불가능해야 한다.

③ 강 일방향성 (Strong onewayness)

⊙ 어떤 서명문 M과 그 해시값 H = h(M)이 주어졌을 때, h(M') = H가 되는 서명문 M' ≠ M을 찾는 것이 계산상 불가능해야 한다.

④ 충돌 회피성 (collision freeness)

⊙ h(M) = h(M')가 되는 서명문 쌍(M, M')(M≠M')을 찾는 것이 계산상 불가능해야 한다.

→ 여기서 ①의 특성은 해시함수의 조건이고, ②, ③, ④의 특성은 해시 함수의 안전성에 관한 제약이다. ②, ③ 특성은 해시 함수의 역함수를 계산하는 것을 방지하는 기능을 말하며, ④ 특성은 서명자가 서명문 M에 서명하여 전송한 후 나중에 M'에 서명하여 전송하였다고 주장하는 이른바 내부 부정을 방지하기 위한 기능이다.

3) 해시 함수의 성질들 사이 관계

① 해시 함수의 성질들 사이에는 다음과 같은 관계가 성립한다.

⊙ 충돌 저항성은 두 번째 역상 저항성을 보장한다.

⊙ 두 번째 역상 저항이 역상 저항을 보장하지 못하며, 역상 저항이 두 번째 역상 저항을 보장하지 못한다.

⊙ 충돌 저항성은 역상 저항성을 보장하지 않는다.

(3) 키가 없는 해시 함수와 키를 사용하는 해시 함수

1) 반복 해시 함수

(A) 기본 개념

① 모든 암호학적 해시 함수는 입력되는 메시지의 크기와 상관없이 항상 일정한 크기의 출력을 내보내야만 한다.

② 이런 함수를 만드는 가장 좋은 방법은 반복을 사용하는 것이다. 입력의 길이가 다양한 해시 함수 대신에 고정 길이의 입력을 필요로 하는 함수를 만들고 필요한 만큼 반복해서 사용하는 것이다.

(B) Merkle-Damgard의 구조

① Merkle-Damgard 구조는 현재 사용되는 많은 암호학적 해시 함수 구조의 기본 틀이다. 우리가 해야 할 한 가지는 바로 충돌 내성을 갖는 압축 함수를 설계해서 Merkle-Damgard 구조 속에 집어넣는 것이다.

② Merkle-Damgard의 구조는 압축 함수가 충돌 내성을 갖게 되는 반복 해시 함수이다.

2) 키가 없는 해시 함수

(A) 기본 개념

① 해시 함수는 내부 압축 함수들로 구성된 연산의 성질에 의해 다음과 같이 세 부분으로 나눌 수 있다.

⊙ 블록 암호를 기초로 한 해시 함수

⊙ 전용 해시 함수 (처음부터 새로 만드는 것)

⊙ 모듈 연산을 기초로 한 해시 함수

(B) 전용 해시 함수

① 오늘날 사용되고 있는 전용 해시 함수인 SHA-1, RIPEMD, RIPEMD-128, RIPEMD-160, HAVAL 등은 모두 MD4를 기초로 디자인 했다.

② 메시지 다이제트(Message Digest)(MD2→MD4→MD5)

⊙ MD 알고리즘에는 MD2, MD4, MD5 이렇게 세 가지가 있는데, RSA를 개발한 미국 MIT의 Rivest 교수가 공개키 기반 구조를 만들기 위해 RSA와 함께 개발했다.

⊙ 최종 버전인 MD5는 메시지를 512비트로 된 블록들로 나누고 128비트 다이제스트를 출력한다. 현재 128비트 다이제스트는 충돌 공격에 내성을 갖기에는 길이가 너무 짧다는 것으로 알려졌다.

⊙ 또한 MD5는 내부 구조에 대한 몇 가지 약점이 발견되고 2005년에는 강한 충돌 내성을 공격하는 생일 공격(Birthday Attack)에 노출되어 보안 요구사항이 높은 응용에는 사용이 권장되지 않고 있다.

③ SHA (Secure Hash Algorithm)

⊙ 가장 널리 사용되는 해시 함수 SHA는 DSS(Digital Signature Standard)에 사용하기 위해 NSA가 설계하였고, NIST에 의해서 배포되었다.

⊙ 2002년에 NIST는 새 표준인 FIPS 180-2를 내놓았는데, 이때 해시값이 각각 256, 384, 512비트인 3개의 새로운 SHA 버전을 정의했다. 각각 SHA-256, SHA-384와 SHA-512이다. 이들 알고리즘을 함께 지칭해서 SHA-2라고 부른다.

⊙ 이 새로운 버전은 SHA-1과 하부 구조가 동일하며 동일한 유형의 모듈러 연산과 논리적 2진 연산을 이용하고 있다. 2008년에 수정된 문서가 FIP PUB 108-3으로 출판되었는데 여기에는 224-비트 버전이 추가되었다.

⊙ 2005년에 SHA-1의 강한 충돌 내성이 깨졌다는 것을 접수하고 NIST는 SHA-1을 대체하는 차세대 일방향 해시 함수 SHA-3을 제정하기로 하였다. SHA-3(Keccak)은 AES와 같은 방식으로 표준화되었다.

구분	SHA-1	SHA-2
구분	SHA-1	SHA-224	SHA-256	SHA-384	SHA-512
MD 길이	160	224	256	384	512
최대 메시지 길이	2⁶⁴-1	2⁶⁴-1	2⁶⁴-1	2¹²⁸-1	2¹²⁸-1
블록 길이	512	512	512	1024	1024
워드 길이	32	32	32	64	64
단계 수	80	64	64	80	80

SHA 해시 알고리즘 비교

중요 체크!

▶ SHA-1의 특징

ⓐ 메시지 길이의 상한 존재

ⓑ 512비트 블록 단위로 처리

▶ LSH

LSH(Lightweight Secure Hash)는 국가 보안 기술 연구소에서 2014년에 개발되어 발표된 경량 해시 함수이다. LSH 해시 함수 군에는 LSH-224/256/384/512 등으로 구성된다.

④ RIPEMD-160

⊙ RIPEMD(Race Integrity Primitives Evaluation Message Digest)도 여러 개의 버전으로 되어있다. RIPEMD-160은 160비트 메시지 다이제스트를 생성하는 해시 알고리즘이다.

⊙ RIPEMD-160은 유럽 RIPE(Race Integrity Primitive Evaluation) 프로젝트로 만들어진 RIPEMD라는 일방향 해시 함수의 개정판이다. RIPEMD의 강한 충돌 내성은 2004년에 깨졌지만, RIPEMD-160은 아직 깨지지 않았다. 한편, RIPEMD-160은 비트 코인에서 사용되고 있다.

⑤ Tiger

⊙ Ross Anderson과 Eli Biham이 1995년에 타이거라고 불리는 해시 함수를 개발하였다. Tiger는 64비트 시스템에서 해시 함수를 수행하기 위해 설계되었고, MD5, SHA-1보다 더 속도가 빠르다.

⑥ HAVAL

⊙ HAVAL은 길이가 128, 160, 192, 224 및 256비트인 메시지 다이제스트를 출력하는 가변 길이 해시 알고리즘이고, 사용되는 블록의 크기는 1024비트이다.

항목	MD5	SHA-1	RIPEMD-160
다이제스트 길이	128비트	160비트	160비트
처리 단위	512비트	512비트	512비트
단계수	64(16번의 4라운드)	80(20번의 4라운드)	160(16번의 5병행 라운드)
최대 메시지 크기	무한(∞)	2⁶⁴－1 비트	2⁶⁴－1 비트
앤디언	Little-endian	Big-endian	Little-endian

주요 해시 알고리즘 비교

① 반복 암호학적 해시 함수 안에 사용되는 압축 함수 자리에 대칭키 블록 암호를 사용할 수도 있다.

② 그러면 일부러 새로운 압축 함수를 만들 필요 없이 DES나 AES처럼 검증된 여러 개의 대칭키 알고리즘을 일방향 함수로 사용할 수 있기 때문이다. 이 경우에는 블록 암호의 암호화 기능만 사용한다.

(D) 모듈 연산에 기반을 둔 해시 함수

① 모듈 연산에 기반을 둔 해시 함수는 압축 함수의 기반을 모듈 연산의 반복적인 수행에 두고 있는 해시 함수를 말한다.

② 이 함수는 하드웨어나 소프트웨어 자체에 내장된 모듈 연산을 사용할 수 있다는 장점이 있으나 속도가 빠르지 않고 안전성 연구에 대한 역사가 짧다는 단점이 있다.

3) 키를 사용하는 해시 함수

(4) 암호학적 해시 함수의 응용

1) 무결성 점검

① 메시지 혹은 문서의 무결성을 점검하기 위해 암호학적 해시 함수를 사용해야 하고, 이렇게 생성된 새로운 메시지 다이제스트와 이전의 메시지 다이제스트를 비교해 보아야 한다.

② 만약 이 두 개가 동일하다면 원래의 메시지가 변경되지 않았다는 것을 확신할 수 있다.

2) 소프트웨어 변경 검출

3) 메시지 인증 코드

4) 전자 서명

(5) 랜덤 오라클 모델과 해시 함수에 대한 공격

1) 랜덤 오라클 모델

(A) 개요

① Bellare와 Rogaway가 1993년에 소개한 랜덤 오라클 모델(Random Oracle Model)은 해시 함수에 대한 이상적인 수학적 모델이다. 이 모델에 근거한 해시 함수는 다음과 같은 성질을 갖는다.

⊙ 임의의 길이를 갖는 메시지에 오라클은 0과 1로 이루어진 난수 스트링인 고정된 길이의 메시지 다이제스트를 생성해서 제공한다.

⊙ 이미 다이제스트가 존재하는 메시지가 주어지면 오라클은 저장되어 있던 다이제스트를 제공한다.

⊙ 새로운 메시지에 대한 다이제스트는 다른 모든 다이제스트와는 독립적으로 선택될 필요가 있다. 이것은 오라클이 다이제스트를 만들기 위해 공식이나 알고리즘을 사용해서는 안 된다는 것을 의미한다.

(B) 비둘기집 원리

① 특정한 해시 값을 생성하는 메시지를 구하는 것이 아니라, 해시값은 뭐든지 괜찮으며, 어쨌든 같은 해시값을 생성하는 2개의 메시지를 구하는 것이다.

② 생일 공격(birthday attack)은 일방향 해시 함수의 「강한 충돌 내성」을 깨고자 하는 공격이다.

③ 생일 패러독스* (birthday paradox)

【생일 퀴즈】 랜덤으로 선택한 N명의 그룹을 생각한다. N명 중 적어도 2명의 생일이 일치할 확률이 「2분의 1」이상이 되도록 하기 위해서는 N이 최저 몇 명이 되어야 할까? (2월 29일은 제외)

【계산법】

「N명 전원의 생일이 일치하지 않을 확률」을 구하고, 그것을 1에서 빼낸다. 1명째는 365일 중 생일이 언제라도 괜찮다. 2명째는 1명째의 생일을 제외한 364일 중 어느날이 생일이다. 3명째는 1명째와 2명째의 생일을 제외한 363일 중 어느날이 생일... N명째는 365 - (N - 1) = 365 - N + 1일 중 어느날이 생일이다. 그러므로 확률은

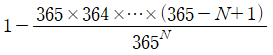
이 된다.

즉, 23명만 있으면 확률이 약 0.507297이 되어 「2분의 1」이상의 확률로 적어도 2명의 생일이 일치한다.

【정답】

N = 23

* 생일 패러독스

- 생일이 「어느날이라도 상관없으므로」 일치할 확률이 상상 이상으로 높아지는 것을 생일 패러독스라고 표현한다.

(D) 랜덤 오라클 모델에 대한 공격

① 무차별 공격에 대한 해시함수의 강도는 전적으로 알고리즘이 생성하는 해시코드의 길이에 달려있다. 길이가 n-비트인 해시코드에 대한 공격의 난이도는 다음과 같이 비례적으로 상승한다.

- n-비트 해시코드에 대한 공격 난이도 표

구분	공격 난이도
프리이미지 저항성	2ⁿ
2차 프리이미지 저항성	2ⁿ
충돌 저항성

② 충돌 공격을 하는 것보다 프리이미지 공격이나 제2 프리이미지 공격을 하는 것이 훨씬 어렵다.